Metode Regula Falsi

Metode regula falsi adalah metode pencarian akar persamaan dengan memanfaatkan kemiringan dan selisih tinggi dari dua titik batas range. Metode ini bekerja secara iterasi dengan melakukan update range. Titik pendekatan yang digunakan oleh metode regula falsi adalah :

Dari nilai x ini perlu dilakukan pengecekan keberadaan akar :

Contoh soal dan listing program : selesaikan persamaan x³+x²-3x-3 = 0 dengan menggunakan range x = (1,9).

Iterasi	a	b	x	f(x)	f(a)	f(b)
1	1	9	1,04081	-3,91165	-4	780
2	1	1,04081	2,84765	19,65806	-4	-3,91165
3	2,84765	1,04081	1,34067	-2,81489	19,65806	-3,91165
4	2,84765	1,34067	1,52942	-1,67162	19,65806	-2,81489
5	2,84765	1,52942	1,63273	3,70485	19,65806	-1,67162

Pada contoh soal diatas hanya mencari jumlah iterasi 5. Sebelum masuk ke listing program, menjelaskan terlebih dahulu tentang algoritma dan flow chart pada metode regula falsi ini. Algoritma metode regula falsi sebagai berikut :

1.      Definisikan fungsi f(x).

2.      Menentukan batas bawah (a) dan batas atas (b).

3.      Menentukan toleransi error  dan iterasi maksimum (n).

4.      Hitung fa = f(a) dan fb=f(b).

5.      Untuk iterasi I = 1 s/d n atau error > .

·        

·         Menghitung fx = f(x).

·         Menghitung error = |fx|.

·         Jika f(x).f(a) < 0 maka b = x dan f(b) = f(x), jika tidak a = x dan f(a) = f(x).

6.      Akar persamaan adalah x.

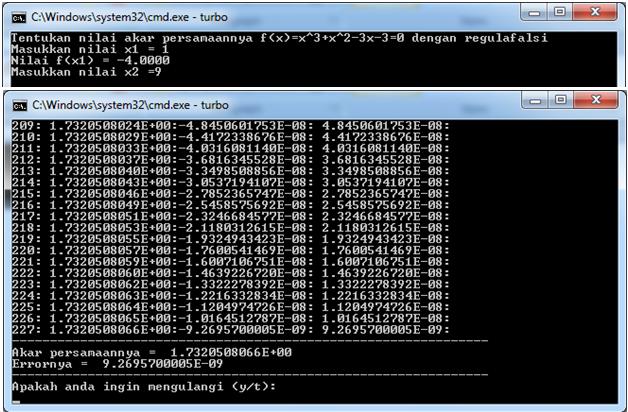
Listing Program Metode Regula Falsi

 Metode Regula Falsi ini mencari nilai dimana iterasi dan kesalahan error dengan akar 10^-7 yang berarti mencari nilai sampai 0.0000001. Dimana pada listing program akan terus looping sampai menemukan persamaan akar dengan memanfaatkan kemiringan dari selisih dari dua titik batas range. Hasil listing program diatas akan tampil pada gambar dibawah ini dengan persamaan f(x) = x³+x²-3x-3=0 dengan range nilai (1,9).

Hasil output pada gambar diatas dimana persamaan f(x) = x³ + x² – 3x – 3 = 0 dengan dua titik batas range (1,9). Dimana akar persamaannya yaitu 1.7320508066E+00 dan toleransi errornya adalah 9.2695700005E-09.